Microeconomics Assignment Analysing Case Of A Beautiful Mind

Question

Task:
Microeconomics Assignment Task:
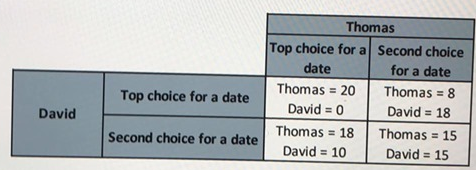
In the movie “A Beautiful Mind”, John Nash, for whom the Nash equilibrium is named, is seated in the university snack shop with friends observing several girls as potential dates. Recognising that one girl would be the first choice of all the men, Nash says that Adam Smith was wrong when he claimed that the group welfare will be maximized when everyone pursues his own self-interest. Assume that the payoff matrix for Thomas and David is as shown below. The choices involve asking the top choice girl for a date or choosing one of the other girls as a second choice. Assume also, as Nash did, that if everyone asks the top choice and one is successful, the other girls will refuse to accept dates since they will know they are second choices. Anyone asking the second choice first will not be rejected since the girl will not know she was second choice.

1. Do Thomas and David have dominant strategies? Why or why not?
2. Is there a Nash equilibrium in this case? Why or why not?
3. If each person adopted a maximum strategy, what would the outcome be?
4. Using the payoff matrix, explain why John Nash felt Adam Smith was wrong in his assertion about social optimal outcome from the pursuit of self-interest.
5. If both Thomas and David were close friends and each seeks the best interest of the other, what will happen and how does this outcome compare with the socially optimal outcome?

Answer

1. It is stated herein microeconomics assignment that in game theory, a dominant strategy implies the optimal move of a person without considering the move of other. A strategy can be said as dominant if by selecting it one can get better outcomes compared to other possible strategies. The dominated strategy does not provide any optimal outcome at any situation (Chen and Li 2018). Therefore, it is a set of actions that results in higher pay off without focusing on opponent’s activity. From the above payoff matrix, it can be observed whether Thomas and David have dominant strategies or not with proper explanation.

   If Thomas selects top choice for a date, David will prefer the second choice. If Thomas selects the second choice, David will prefer the top choice. Hence, David does not have any dominant strategy. On the other side, if David selects top choice for a date, Thomas will prefer top choice as well. If David prefers to select second choice, Thomas will prefer top choice. Therefore, Thomas has the dominating strategy.

2. A Nash equilibrium is an essential concept as it gives outcome of a situation where every participant wins as they achieve the outcome they want. Hence, it is a decision-making theorem in game theory which describes that a player can successfully get the desired outcome by remaining at their initial strategy (Liang, Yi and Hong 2017). Thus, each player’s strategy is considered as optimal at the time of considering other players’ decisions.

   The case has a Nash equilibrium at the point where Thomas will select top choice for a date and David will select second choice for a date. At this point, both Thomas and David will get their optimal outcome and they will not prefer to shift from there. For obtaining this equilibrium, action profile of each of them is considered (Reny 2016). By calculating dominant strategy, it is seen that at this action profile, no players can increase their payoff by selecting any other action. Therefore, it is proved that this payoff is actually the Nash equilibrium for this game.

3. In game theory, a maximin strategy is a strategy that helps a player to make decision for making the best of the worst outcome. Each decision in the game theory has benefits and costs. The strategy helps to find out the decision that makes the smallest cost (Ismail 2019). If Thomas and David apply this maximin strategy then the outcome would be as follow:

   In case of top choice for a date, the minimum strategy for David is 0. In case of second choice for a date, the minimum strategy of him is 15. Considering these two choices, it is seen that the maximum choice for David is 15, which is to choose second for a date. On the other side, the minimum strategy of Thomas for top choice for a date is 18. The minimum strategy for second choice for a date is 8. Considering these, it can be seen that the maximum choice for Thomas is second choice for a date.

4. Self-interest leads a person to take actions for produce personal interest. According to Adam Smith, the best benefit from economic point of view can be accomplished if an individual work on self-interest. From his concept of “invisible hand” it is understood that if people act on their self-interest with economic rationality, consumers and producers will get benefit from the goods and services (Khalil 2019). Behavioural decisions influence well-being as well as personal income of those person when they in an economically rational way. Self-interest can be considered from both economic and psychological perspective. It implies actions and behaviours of an individual that influence positive personal benefit.

   However, as per the given situation of the movie, Nash felt that the assertation of Adam Smith was wrong regarding social optimal outcomes where an invisible hand operates from the pursuit of self-interest. Here, everyone is asking for top choice girl for a date and looking for second choice if top choice is selected. Here, people who are selecting second choice are not getting the option tofulfilling their self-interest. On the other side, girls are also rejected after knowing that they are second choice. Thus, as per the concept of invisible hand, here both girls and boys are not benefitted as per their requirements.

5. If Thomas and David were close friends they will not think about their self-interest. Rather, they will think about the interest of other each other. In this context, both Thomas and David could reject the top choice for a date and will select other girls as the second choice for a date so that no one would feel better compared to another. According to socially optimal outcome, the resources are distributed optimally in society by considering all external benefits and costs along with internal benefits and costs (Redko and Laclau 2019). Therefore, in the given situation, Thomas and David will think about their cost benefit regarding their friendship and will come to the decision. Here, Nash equilibrium is not socially optimal as Thomas was strict on his top choice. However, in case of good friends, this decision will be changed.

References:
Chen, Y.C. and Li, J., 2018. Revisiting the foundations of dominant-strategy mechanisms. Journal of Economic Theory, 178, pp.294-317.

Ismail, M., 2019. Maximin equilibrium. arXiv preprint arXiv:1912.00211.

Khalil, E.L., 2019. Is the Adulation of the Rich-and-Powerful Derived from Benevolence? Adam Smith and the Distinction Between Aspiration and Interests. Critical Horizons, 20(4), pp.285-304.

Liang, S., Yi, P. and Hong, Y., 2017. Distributed Nash equilibrium seeking for aggregative games with coupled constraints. Microeconomics assignment Automatica, 85, pp.179-185.

Redko, I. and Laclau, C., 2019, July. On Fair Cost Sharing Games in Machine Learning. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 33, pp. 4790-4797).

Reny, P.J., 2016. Nash equilibrium in discontinuous games. Economic Theory, 61(3), pp.553-569.