Algorithm Assignment: Scheduling Algorithm For LPG Distribution By SaO Gas Ltd
Question
Task:
In this algorithm assignment you will address a real-world problem of delivery planning for the LPG (Liquefied Petroleum Gas) distributor. In the areas where mains gas for heating purposes is not available, LPG is the closest alternative. It has the lowest carbon emissions per kWh out of all fossil fuels available in rural areas, does not pose any ground or water pollution hazards and can be used for both heating and cooking. LPG distribution companies source the fuel from major oil refineries and deliver it to the bulk customers by a fleet tanker lorries.
You have been employed by SaO Gas Ltd as data scientists. You are to produce delivery schedules for the fleet of 25 tanker lorries operating from 4 depots in the country of Optilandia (which surprisingly use £ as their currency), minimizing the overall cost of delivery for the distributor under certain constraints.
Answer
Optimization algorithms are deemed to be a very complicated task since it involves unbiased comparison of several algorithms. In this algorithm assignment we are going to perform an algorithm optimization problem where we will use the python scripts and algorithms. There are several optimization methods that can be implemented in this case. The optimization methods will all rely on the types of algorithms that have been used. That said, we do have 6 types of algorithms that can be used in scheduling. This includes; First Come First Serve (FCFS), Shortest-Job-First (SJF), Shortest Remaining Time (SRT), Priority Scheduling (PS) and the Round Robin Scheduling (RRS). The First Come First Serve Algorithm technique means that the process that makes the request first gets the first allocations. In the Shortest Remaining Time the process that is allocated the task is one that is closest to completion. The priority scheduling algorithm means that the scheduler or in this case the python tool will have to select the tasks that are being given the highest priority. In our case the LPG gas is the only product being transported and thus the destination will be the priority when scheduling using thus algorithm. In this paper we are going to implement at least two optimization schemes that will address the delivery scheduling problem.
Problem Definition
In this paper we are going to use scheduling algorithms to solve the real world problems. Using these algorithms, we are going to plan on how deliveries of the LPG for a distributor can be done. Our distribution company is the SaO Gas Ltd. There are 25 tankers operating from the 4 depots in the country of Optilandia. The distribution that we are supposed to adopt is supposed to cut down the costs of distributing LPG.
The type of tankers that is operated by the company includes;
|
Tanker Type |
Capacity [Tonnes] |
Cost Per Mile [?] |
Cost Per Mile per tonne [?] |
|
Small |
5 |
1.00 |
1.50 |
|
Medium |
12 |
1.50 |
1.00 |
|
Large |
22 |
2.00 |
0.50 |
The above table can be analyzed in the form, with the assumption that the depots don’t run out of LPG, a tanker loaded with 22 tonnes of LPG can incur the following costs.

The table below shows the depots that the company operates under.
|
Depot |
Location ID |
Small Tankers |
Medium Tankers |
Large Tankers |
|
1 |
#523 |
2 |
2 |
1 |
|
2 |
#124 |
3 |
3 |
2 |
|
3 |
#373 |
3 |
4 |
3 |
|
4 |
#116 |
1 |
1 |
0 |
Here is the map of the deliveries;
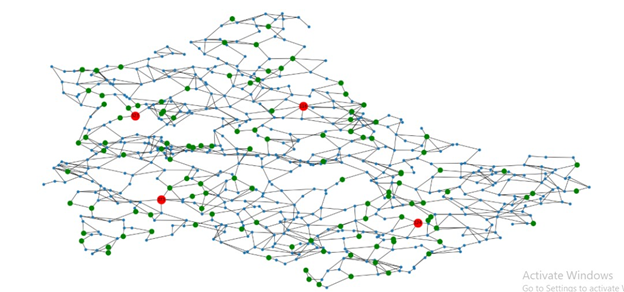
In the map shown above the red dots indicate the location of the four depots. On the other hand the green dots denote the location of the SaO gas customers.
From the above information we are supposed to provide solution to the following problems;
- Write a python algorithm that will schedule for the delivery of the LPG to all the customers as it minimizes the overall cost of delivery. We are going to assume an ideal situation that has no additional constrains apart from the tanker lorry capacity.
- Schedule LPG delivery with the objective of maximizing the amount of gas deliveries to the customers. Under this we are going to observe the following constraints;
- Each lorry can only travel up to 250 miles
- Each lorry can have a maximum of 5 stop over which includes customer deliveries and additional visits back to the depot
- Each of the lorry must end up the journey to the depots.
- If no deliveries are made to customers who have less than 15 % of gas in their tanks then SaO Ltd will incur a penalty of ? 1000.
To provide the solution to the above problems then we will need to design two optimization schemes to address this. We are going to use random and the greedy scheduler so as to generate a valid solution. When implementing the solution we are not going to violate the constraints put in place. The scheduler that we developed is based on both the genetic algorithms and Ant Colony Optimization.
Methodology
To provide the solution to the above problems then we will need to design two optimization schemes to address this. We are going to use random and the greedy scheduler so as to generate a valid solution. When implementing the solution we are not going to violate the constraints put in place. The scheduler that we developed is based on both the genetic algorithms and Ant Colony Optimization. The purpose of this paper is to use the Genetic Algorithm approach to solve the problem of two optimization schemes. Genetic Algorithm was first introduced by Holland and the main of their abstract was to provide adaptive techniques for the natural systems and create artificial system to solve the scheme problems.
- The truck routing and scheduling problem that is presented in this paper can be described as below. Write a python algorithm that will schedule for the delivery of the LPG to all the customers as it minimizes the overall cost of delivery. We are going to assume an ideal situation that has no additional constrains apart from the tanker lorry capacity.
- Schedule LPG delivery with the objective of maximizing the amount of gas deliveries to the customers. Under this we are going to observe the following constraints;
- Each lorry can only travel up to 250 miles
- Each lorry can have a maximum of 5 stop overs which includes customer deliveries and additional visits back to the depot
- Each of the lorry must end up the journey to the depots.
- If no deliveries are made to customers who have less than 15 % of gas in their tanks then SaO Ltd will incur a penalty of ? 1000.
To provide the solution to the above problems then we will need to design two optimization schemes to address this. We are going to use random and the greedy scheduler so as to generate a valid solution. When implementing the solution we are not going to violate the constraints put in place. The scheduler that we developed is based on both the genetic algorithms and Ant Colony Optimization.
To develop the Genetic Algorithm we had to consider the following notations;
Data

Decision Variables.
The decision variables are determined by the constraints that are set. These constraints include;
- Each lorry can only travel up to 250 miles
- Each lorry can have a maximum of 5 stop overs which includes customer deliveries and additional visits back to the depot
- Each of the lorry must end up the journey to the depots.
- If no deliveries are made to customers who have less than 15 % of gas in their tanks then SaO Ltd will incur a penalty of ? 1000.
From the mentioned constraints we will set the following decision variables;

From that we therefore used the following algorithm code that solved the above problem;

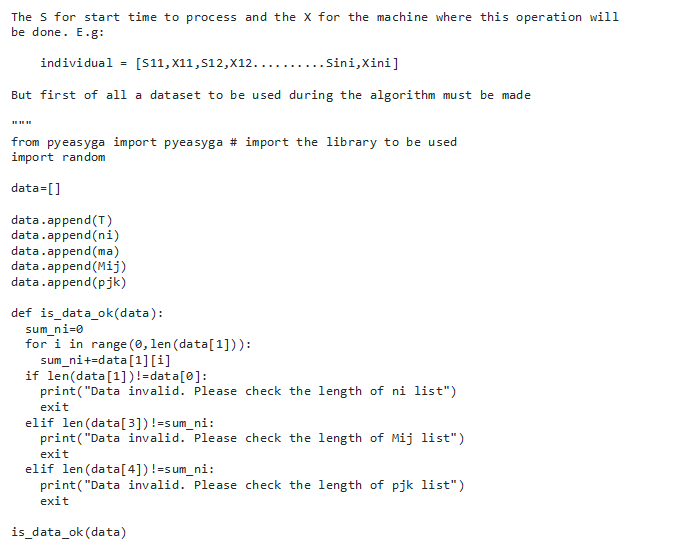


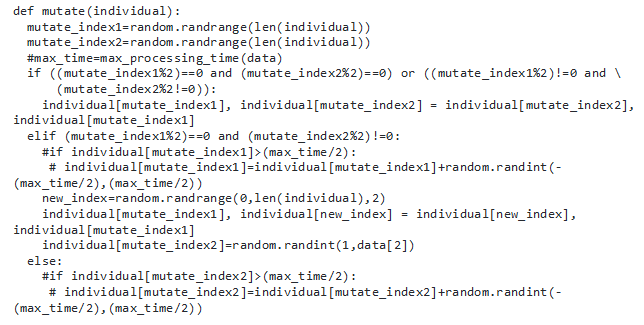
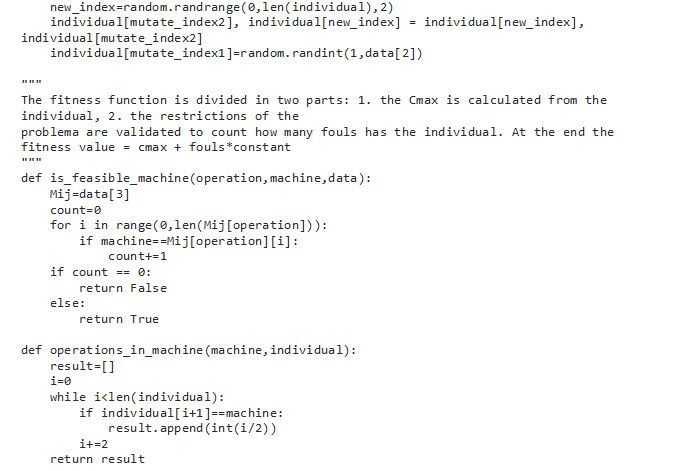
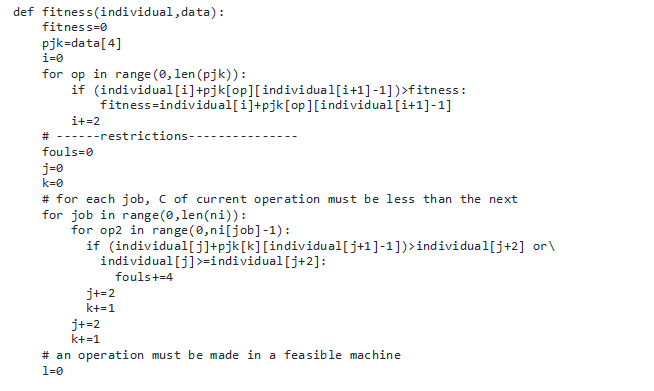
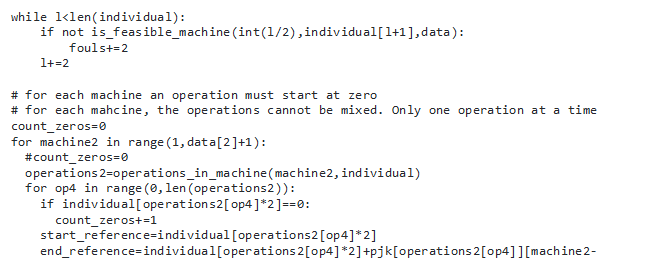
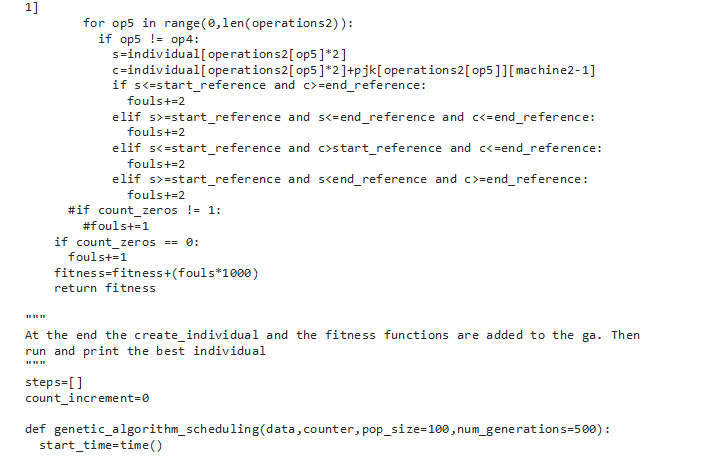

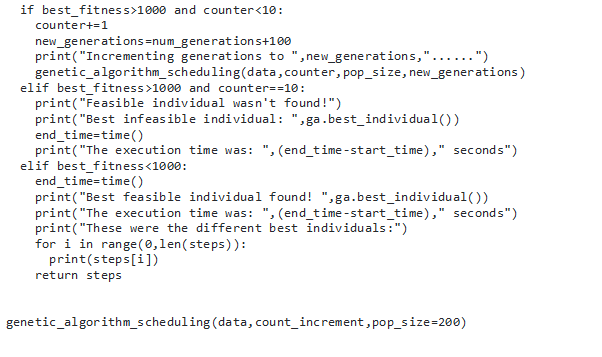
Results and Discussion

From the above r will be set to be our objective which includes;
- The truck routing and scheduling problem that is presented in this paper can be described as below. Write a python algorithm that will schedule for the delivery of the LPG to all the customers as it minimizes the overall cost of delivery. We are going to assume an ideal situation that has no additional constrains apart from the tanker lorry capacity.
- Schedule LPG delivery with the objective of maximizing the amount of gas deliveries to the customers.
Implementation of the algorithm.
The genetic implementation of the above algorithm is based on the version that Syswerda terms as “Steady State” genetic algorithm. The initial population of the trucks and the customers was created randomly based on the CSV Data files that were created. The production process based on the profits was continuous until a convergence was reached that is 95% of the customers had been delivered the LPG Gas. The indexing was also ranked. This was done using the Genetic algorithm pseudo code from Whitley et al.

|
import java.util.Random; |
|
|
|
|
|
/** |
|
|
* |
|
|
* @author Collins |
|
|
*/ |
|
|
|
|
|
//Main class |
|
|
publicclassSimpleDemoGA { |
|
|
|
|
|
Population population =new Population(); |
|
|
Individual fittest; |
|
|
Individual secondFittest; |
|
|
int generationCount =0; |
|
|
|
|
|
publicstaticvoidmain(String[] args) { |
|
|
|
|
|
Random rn =new Random(); |
|
|
|
|
|
SimpleDemoGA demo =new SimpleDemoGA(); |
|
|
|
|
|
//Initialize population |
|
|
demo.population.initializePopulation(10); |
|
|
|
|
|
//Calculate fitness of each individual |
|
|
demo.population.calculateFitness(); |
|
|
|
|
|
System.out.println("Generation: "+ demo.generationCount +" Fittest: "+ demo.population.fittest); |
|
|
|
|
|
//While population gets an individual with maximum fitness |
|
|
while (demo.population.fittest <5) { |
|
|
++demo.generationCount; |
|
|
|
|
|
//Do selection |
|
|
demo.selection(); |
|
|
|
|
|
//Do crossover |
|
|
demo.crossover(); |
|
|
|
|
|
//Do mutation under a random probability |
|
|
if (rn.nextInt()%7<5) { |
|
|
demo.mutation(); |
|
|
} |
|
|
|
|
|
//Add fittest offspring to population |
|
|
demo.addFittestOffspring(); |
|
|
|
|
|
//Calculate new fitness value |
|
|
demo.population.calculateFitness(); |
|
|
|
|
|
System.out.println("Generation: "+ demo.generationCount +" Fittest: "+ demo.population.fittest); |
|
|
} |
|
|
|
|
|
System.out.println("\nSolution found in generation "+ demo.generationCount); |
|
|
System.out.println("Fitness: "+demo.population.getFittest().fitness); |
|
|
System.out.print("Genes: "); |
|
|
for (int i =0; i <5; i++) { |
|
|
System.out.print(demo.population.getFittest().genes[i]); |
|
|
} |
|
|
|
|
|
System.out.println(""); |
|
|
|
|
|
} |
|
|
|
|
|
//Selection |
|
|
voidselection() { |
|
|
|
|
|
//Select the most fittest individual |
|
|
fittest = population.getFittest(); |
|
|
|
|
|
//Select the second most fittest individual |
|
|
secondFittest = population.getSecondFittest(); |
|
|
} |
|
|
|
|
|
//Crossover |
|
|
voidcrossover() { |
|
|
Random rn =new Random(); |
|
|
|
|
|
//Select a random crossover point |
|
|
int crossOverPoint = rn.nextInt(population.individuals[0].geneLength); |
|
|
|
|
|
//Swap values among parents |
|
|
for (int i =0; i < crossOverPoint; i++) { |
|
|
int temp = fittest.genes[i]; |
|
|
fittest.genes[i] = secondFittest.genes[i]; |
|
|
secondFittest.genes[i] = temp; |
|
|
|
|
|
} |
|
|
|
|
|
} |
|
|
|
|
|
//Mutation |
|
|
voidmutation() { |
|
|
Random rn =new Random(); |
|
|
|
|
|
//Select a random mutation point |
|
|
int mutationPoint = rn.nextInt(population.individuals[0].geneLength); |
|
|
|
|
|
//Flip values at the mutation point |
|
|
if (fittest.genes[mutationPoint] ==0) { |
|
|
fittest.genes[mutationPoint] =1; |
|
|
} else { |
|
|
fittest.genes[mutationPoint] =0; |
|
|
} |
|
|
|
|
|
mutationPoint = rn.nextInt(population.individuals[0].geneLength); |
|
|
|
|
|
if (secondFittest.genes[mutationPoint] ==0) { |
|
|
secondFittest.genes[mutationPoint] =1; |
|
|
} else { |
|
|
secondFittest.genes[mutationPoint] =0; |
|
|
} |
|
|
} |
|
|
|
|
|
//Get fittest offspring |
|
|
Individual getFittestOffspring() { |
|
|
if (fittest.fitness > secondFittest.fitness) { |
|
|
return fittest; |
|
|
} |
|
|
return secondFittest; |
|
|
} |
|
|
|
|
|
|
|
|
//Replace least fittest individual from most fittest offspring |
|
|
voidaddFittestOffspring() { |
|
|
|
|
|
//Update fitness values of offspring |
|
|
fittest.calcFitness(); |
|
|
secondFittest.calcFitness(); |
|
|
|
|
|
//Get index of least fit individual |
|
|
int leastFittestIndex = population.getLeastFittestIndex(); |
|
|
|
|
|
//Replace least fittest individual from most fittest offspring |
|
|
population.individuals[leastFittestIndex] = getFittestOffspring(); |
|
|
} |
|
|
|
|
|
} |
|
|
|
|
|
|
|
|
//Individual class |
|
|
classIndividual { |
|
|
|
|
|
int fitness =0; |
|
|
int[] genes =new int[5]; |
|
|
int geneLength =5; |
|
|
|
|
|
publicIndividual() { |
|
|
Random rn =new Random(); |
|
|
|
|
|
//Set genes randomly for each individual |
|
|
for (int i =0; i < genes.length; i++) { |
|
|
genes[i] = Math.abs(rn.nextInt() %2); |
|
|
} |
|
|
|
|
|
fitness =0; |
|
|
} |
|
|
|
|
|
//Calculate fitness |
|
|
publicvoidcalcFitness() { |
|
|
|
|
|
fitness =0; |
|
|
for (int i =0; i <5; i++) { |
|
|
if (genes[i] ==1) { |
|
|
++fitness; |
|
|
} |
|
|
} |
|
|
} |
|
|
|
|
|
} |
|
|
|
|
|
//Population class |
|
|
classPopulation { |
|
|
|
|
|
int popSize =10; |
|
|
Individual[] individuals =new Individual[10]; |
|
|
int fittest =0; |
|
|
|
|
|
//Initialize population |
|
|
publicvoidinitializePopulation(intsize) { |
|
|
for (int i =0; i < individuals.length; i++) { |
|
|
individuals[i] =new Individual(); |
|
|
} |
|
|
} |
|
|
|
|
|
//Get the fittest individual |
|
|
public Individual getFittest() { |
|
|
int maxFit = Integer.MIN_VALUE; |
|
|
int maxFitIndex =0; |
|
|
for (int i =0; i < individuals.length; i++) { |
|
|
if (maxFit <= individuals[i].fitness) { |
|
|
maxFit = individuals[i].fitness; |
|
|
maxFitIndex = i; |
|
|
} |
|
|
} |
|
|
fittest = individuals[maxFitIndex].fitness; |
|
|
return individuals[maxFitIndex]; |
|
|
} |
|
|
|
|
|
//Get the second most fittest individual |
|
|
public Individual getSecondFittest() { |
|
|
int maxFit1 =0; |
|
|
int maxFit2 =0; |
|
|
for (int i =0; i < individuals.length; i++) { |
|
|
if (individuals[i].fitness > individuals[maxFit1].fitness) { |
|
|
maxFit2 = maxFit1; |
|
|
maxFit1 = i; |
|
|
} elseif (individuals[i].fitness > individuals[maxFit2].fitness) { |
|
|
maxFit2 = i; |
|
|
} |
|
|
} |
|
|
return individuals[maxFit2]; |
|
|
} |
|
|
|
|
|
//Get index of least fittest individual |
|
|
publicintgetLeastFittestIndex() { |
|
|
int minFitVal = Integer.MAX_VALUE; |
|
|
int minFitIndex =0; |
|
|
for (int i =0; i < individuals.length; i++) { |
|
|
if (minFitVal >= individuals[i].fitness) { |
|
|
minFitVal = individuals[i].fitness; |
|
|
minFitIndex = i; |
|
|
} |
|
|
} |
|
|
return minFitIndex; |
|
|
} |
|
|
|
|
|
//Calculate fitness of each individual |
|
|
publicvoidcalculateFitness() { |
|
|
|
|
|
for (int i =0; i < individuals.length; i++) { |
|
|
individuals[i].calcFitness(); |
|
|
} |
|
|
getFittest(); |
|
|
} |
|
|
|
|
|
} |
|
Using the coding above the chromosomes were coded and decoded using the MDCVRP as sequence problem. One chromosome in the population is made of (NC-2*NV) customers. Using the decoding procedure was used to convert the orders into the routes for the trucks that are done as following.
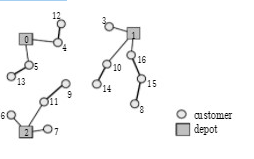
The figure above shows the decoding procedure that starts off by the first customer in the chromosome one after another customer is connected to the currently closest half of the track route. From that the cost was saved because they were able to provide the exact results.
Conclusion
The fixed destination of the multiple depots incapacitated the track routing problem that has been solved in this paper. The paper provides a step by step knowledge that solved the problems mentioned below. Write a python algorithm that will schedule for the delivery of the LPG to all the customers as it minimizes the overall cost of delivery. We are going to assume an ideal situation that has no additional constrains apart from the tanker lorry capacity. Schedule LPG delivery with the objective of maximizing the amount of gas deliveries to the customers. The algorithms are highly flexible to provide solution to the model problem. A lot of research still has to be done on these techniques.
References
H. Osman, Vehicle Routing and Scheduling: Applications, Algorithms and Developments, Proceedings of the International Conference on Industrial Logistic, 1993, Rennes, France.
L. Bodin, B. Golden, A. Assad, M. Ball, The State of the Art in the Routing and Scheduling of Vehicles and Crews, Computers and Operations Research, Vol.10, 1983, pp.63-211.
G. Laporte, The Vehicle Routing Problem: An Overview of Exact and Approximate Algorithms, European Journal of Operations Research, Vol.59, 1992, pp.345-358.
G. Laporte, Y. Nobert, D. Arpin, Optimal solutions of routing problem, Congressus Numeratium, Vol.44, 1984, pp. 283-292. [5] F. A. Tillman, R. W. Hering, A study of look-ahead procedure for solving the multi-terminal delivery problem, Transportation Research, Vol.5, 1971, pp. 225-229.
A. Wren, A. Holliday, Computer scheduling of vehicles from one or more delivery points, Operational Research, Vol.23, 1972, pp.333-334. [7] B. Golden, T. L. Magnanti, H. Q. Nguyen, Implementing vehicle routing algorithms, Networks, Vol.7, 1977, pp. 113-148.
I. M. Chao, B. L. Golden, E. A. Wasil, A new heuristic for multiple-depot vehicle routing problem that improves upon best-known solutions, Algorithm assignment American Journal of Mathematical and Management Sciences, Vol.13, 1993, pp.371-406.
J. Renaud, F. F. Boctor, G. Laporte, An improved petal heuristic for the vehicle routing problem, Journal of the Operational Research Society, Vol.47, 1996, pp.329-336.
S.Krajcar, Algorithms for Interactive Optimal Planing of Distribution Networks, Doctoral thesis, Faculty of Electrical Engineering and Computing, University of Zagreb, 1988.
M. Filipec, D. Skrlec, S. Krajcar, Darwin meets computers: New approach to multiple depot capacitated vehicle routing problem, Proceedings of International Conference on Systems, Man and Cybernetics, Orlando, USA, October, 1997, pp.421-426.
M. Filipec, D. Skrlec, S. Krajcar, Genetic Algorithm Approach For Multiple Depot Capacitated Vehicle Routing Problem Solving With Heuristic Improvements Built-in, International Journal of Modeling and Simulation, Vol. 20, No. 4, 2000, pp.320-327.
D.Whitley, The Genitor Algorithm and Selection Pressure: Why Rank-Based Allocation of Reproductive Trials is Best, Proceedings of ICGA '89, 1989, pp.116-121.
A. Homaifair, S.H.-Y.Lai, X. Qi, Constrained Optimization via Genetic Algorithms, Simulation, Vol.62, 1994, pp.242-254. J. A. Joines, C. R. Houck, On the Use of Non-Stationary Penalty Functions to Solve Nonlinear Constrained Optimization Problems With GAs, Proceedings of the First International Conference on Evolutionary Computation, Orlando, June, 1994, pp.579-584.